A class of chaotic systems with variable attractors have been recently proposed. The location of chaotic attractor is variable on phase space and it can be chosen arbitrarily according to offset control parameters.
A fractional order dynamical system is considered as a generalization of the integer-order versions. Several works showing the fractional order form of well-known chaotic systems such as Chua system, Chen, Lorenz and so on, were reported. Also, new chaotic systems with fractional derivatives have been proposed. The main research interest is related to hereditary properties, i.e., memory, that the fractional order dynamical systems can exhibit. Indeed, those special features are very useful to describe more accurately many real world phenomena in different fields such as biology, economics, botany, hidden dynamics, digital circuits, cryptography, ciphers, control, telecommunications, image processing, wind turbines, viscoelastic studies, ferroelectric materials, and so forth.
A novel fractional order dynamical system with a variable double-scroll attractor on a line, lattice and 3D grid is studied. This system belongs to a class of chaotic systems with adjustable variables but with fractional order. Chaos generation only depends on the value of fractional order. As a result, a chaotic attractor is discovered and propagated in y-line. By introducing two extra control parameters, we also observed that the chaotic attractor varies in x-line, z-line, x − y-lattice, x − z-lattice, y − z-lattice, and 3D- grid.
Additionally, a class of chaotic systems with variable attractors have been recently proposed. These systems are pointed out as a proper solution for chaos-based applications since it can reduce the number of electronic components required for signal conditioning due to the chaotic signals can be designed with any polarity. It means that the location of chaotic attractor is variable on phase space and it can be chosen arbitrarily according to offset control parameters.
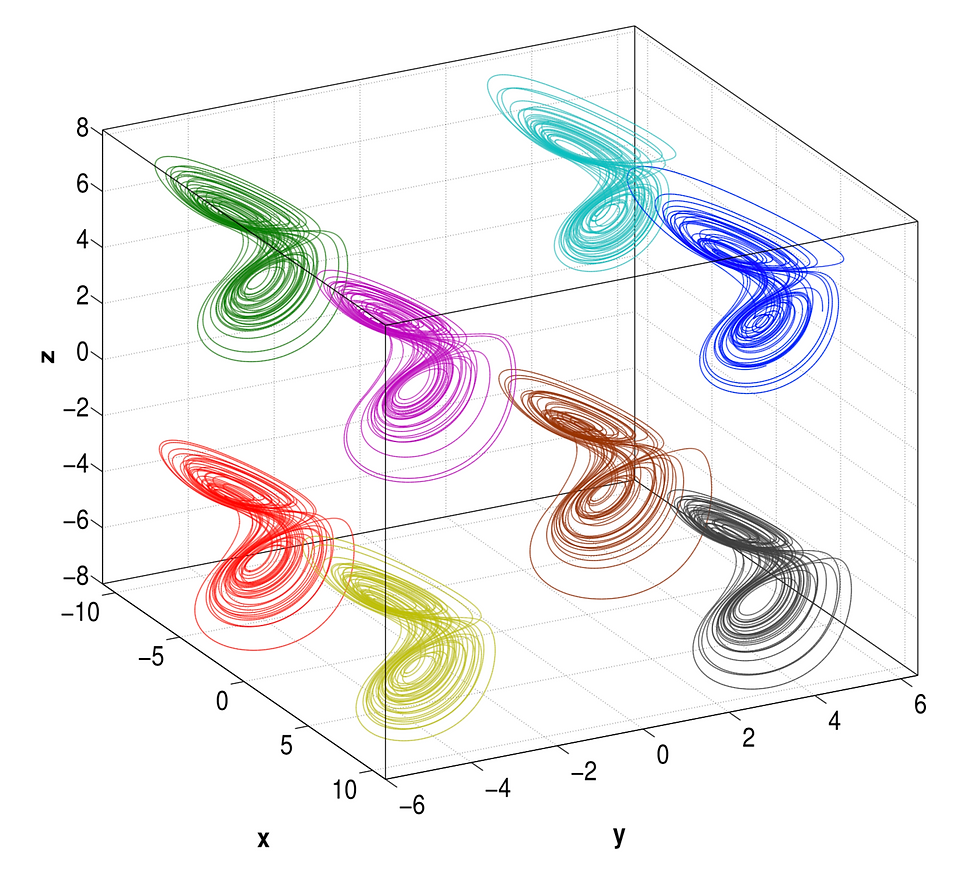
The observed chaotic behavior was only valid for the fractional order domain. Indeed, chaos disappeared for the integer- order scenario. It was concluded that an imperfect order (fractional order) stimulates the emergence of an unseen chaotic dynamics.
For details consult:
Munoz-Pacheco, J. M., Zambrano-Serrano, E., Volos, C., Tacha, O. I., Stouboulos, I. N., & Pham, V. T. (2018). A fractional order chaotic system with a 3D grid of variable attractors. Chaos, Solitons & Fractals,113, 69-78.