top of page
Chaotic systems with hidden and self-excited attractors
Description

Here, we study chaotic systems both integer- and fractional-order, which can generate hidden and self-excited attractors. We use several dynamical analysis to discover all the behaviors. We are interested in particular in proposing new systems, which can satisfy the following:

​

  • The system should credibly model some important unsolved problems in nature.

  • The system should exhibit some behavior previously unobserved.

  • The system should be simpler than all other known examples exhibiting the observed behavior.

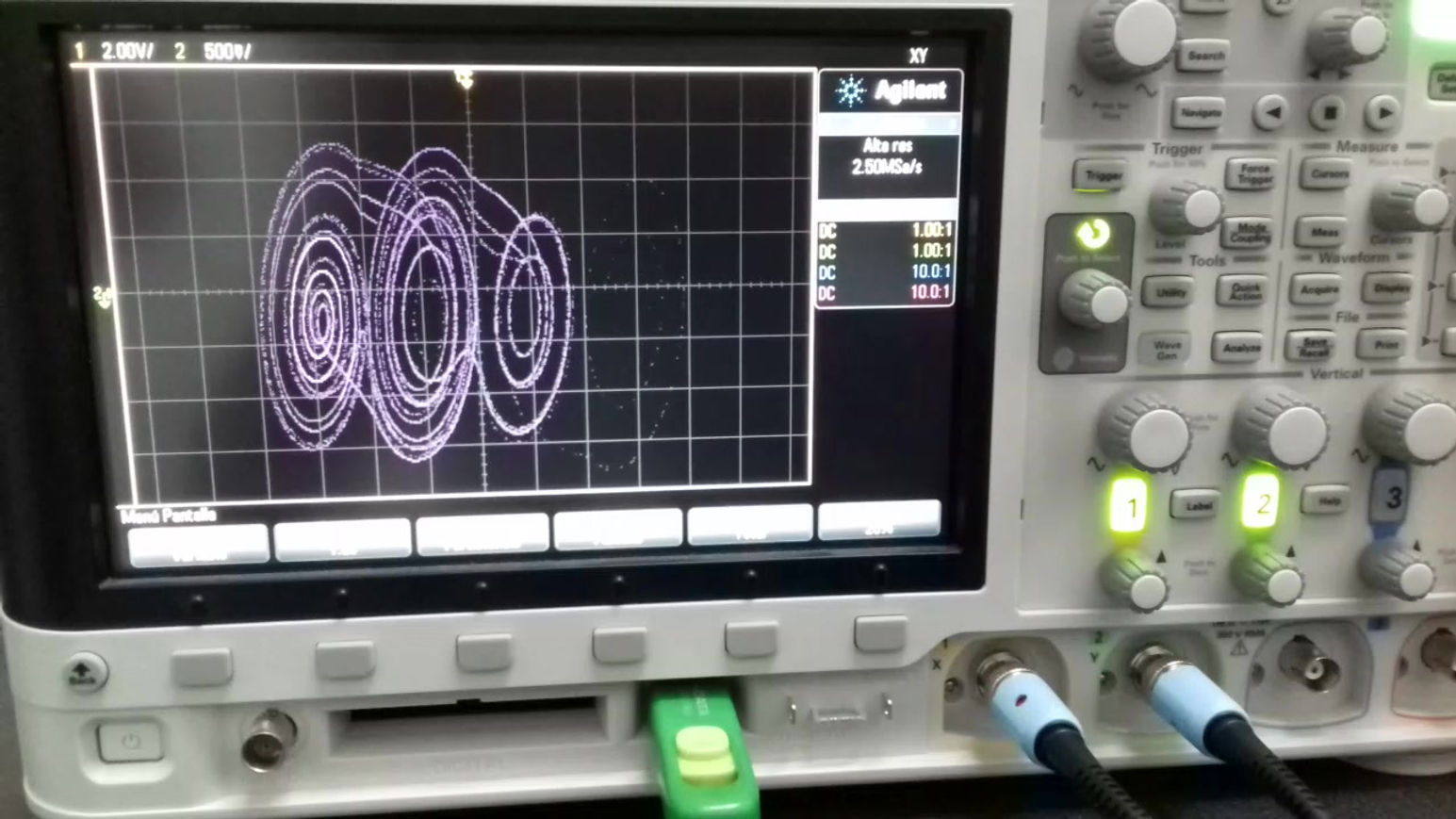
20171010_144003
Reproducir video
Some related publications

  • Munoz-Pacheco, J., Zambrano-Serrano, E., Volos, C., Jafari, S., Kengne, J., & Rajagopal, K. (2018). A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy, 20(8), 564.

  • Tacha, O. I., Munoz-Pacheco, J. M., Zambrano-Serrano, E., Stouboulos, I. N., & Pham, V. T. (2018). Determining the chaotic behavior in a fractional-order finance system with negative parameters. Nonlinear Dynamics, 94(2), 1303-1317.

  • J.M. Muñoz-Pacheco, D.K. Guevara-Flores, O.G. Félix-Beltran, E. Tlelo-Cuautle, J.E. Barradas-Guevara, C.K. Volos; Experimental Verification of Optimized Multiscroll Chaotic Oscillators Based on Irregular Saturated Functions, Complexity, volumen 2018, article ID 3151840, 17 pp., 2018-04-25, 2018.​

Fractional-order nonlinear dynamical systems
Description
MVI_9691
Reproducir video

Since fractional calculus has important mathematical formulations and engineering applications due to their memory effect, we aim for studying:
 

  • The implications of fractional-order in nonlinear dynamical systems by using typical definitions for fractional derivatives, such as Caputo, Riemann-Liouville, and Grunwald-Letnikov.

  • The dynamics of classes of chaotic systems, biological systems, economical systems, and so on. 

  • The numerical algorithms for computing time-response, bifurcation diagrams, Lyapunov exponents, basins of attraction, etc.

Some related publications

  • Montero-Canela, R., Zambrano-Serrano, E., Tamariz-Flores, E. I., Muñoz-Pacheco, J. M., & Torrealba-Meléndez, R. (2020). Fractional chaos based-cryptosystem for generating encryption keys in Ad Hoc networks. Ad Hoc Networks, 97, 102005.

  • Muñoz-Pacheco, J. M. (2019). Infinitely many hidden attractors in a new fractional-order chaotic system based on a fracmemristor. The European Physical Journal Special Topics, 228(10), 2185-2196.

  • Munoz-Pacheco, J. M., Zambrano-Serrano, E., Volos, C., Tacha, O. I., Stouboulos, I. N., & Pham, V. T. (2018). A fractional order chaotic system with a 3D grid of variable attractors. Chaos, Solitons & Fractals, 113, 69-78.

Circuit implementation
(analog and digital)
Description

The engineering applications demand physical realizations of fractional- and integer-order dynamical systems. Therefore, we focus on:

​

  • The design of analog circuits (FPAAs, OpAmps) for implementing fractional-order integrators and chaotic systems.

  • The design of digital circuits (FPGAs, ARM, DSPs) for implementing fractional-order approximations and digital chaotic systems.

  • The design of Application Specific Integrated Circuits (ASICs) for implementing chaotic systems.

IMG-20180814-WA0022_edited.jpg
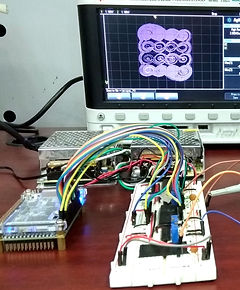
2scrolls2_edited.jpg
Some related publications

  • Munoz-Pacheco, J. M., García-Chávez, T., Gonzalez-Diaz, V. R., de La Fuente-Cortes, G., & del Carmen Gómez-Pavón, L. (2020). Two New Asymmetric Boolean Chaos Oscillators with No Dependence on Incommensurate Time-Delays and Their Circuit Implementation. Symmetry, 12(4), 506.

  • E. Zambrano-Serrano, J. M. Munoz–Pacheco, E. Campos-Cantón; Chaos generation in fractional-order switched systems and its digital implementation, AEÜ International Journal of Electronics and Communications, 79 pp. 43-52. ISSN: 1434-8411, 2017.

  • J.M. Munoz-Pacheco, E. Tlelo-Cuautle, I. Toxqui-Toxqui, C. Sánchez-López, R. Trejo-Guerra; Frequency limitations in generating multi-scroll chaotic attractors using CFOAs. International Journal of Electronics, 101(11) pp. 1559-1569. ISSN:0020-7217, 2014.

Synchronization of chaotic and fractional-order systems
Description

The synchronization process is almost ubiquitous in nature. Several phenomena are synchronized for functioning in a variety of forms. In this manner, our goals are:

​

  • The control techniques to achieve the synchronization of dynamical systems.

  • The numerical algorithms to characterize the synchronization process.

  • The physical realizations of the control algorithms.

Some related publications

  • Zambrano-Serrano, E., Muñoz-Pacheco, J. M., Gómez-Pavón, L. C., Luis-Ramos, A., & Chen, G. (2018). Synchronization in a fractional-order model of pancreatic β-cells. The European Physical Journal Special Topics, 227(7-9), 907-919.

  • L.C. Gómez-Pavón, J.M. Munoz-Pacheco, A. Luis-Ramos; Synchronous chaos generation in an Er3+-Doped fiber laser system, IEEE Photonics Journal, 7(2) pp.1-7. ISSN:1943-0655, 2015.

  • J.M. Munoz-Pacheco, E. Zambrano-Serrano, O. Félix-Beltrán, L.C. Gómez-Pavón, A. Luis-Ramos; Synchronization of PWL function-based 2D and 3D multi-scroll chaotic systems. Nonlinear Dynamics, 70(2) pp. 1633-1643. ISSN:0924-090X, 2012

bottom of page